2d20/2 (how to average dice rolls)

Baldur's Gate 3 has been released after 6 years of development (including 3 years of early access). While I prefer RTWP to turn-based combat, being the grandest CRPG ever made is enough reason for me to try it. But I'm in no hurry. The game can only improve over time through patches and mods.

The game system is largely based on Dungeons & Dragons 5th edition rule set (DnD 5e). A prominent feature of DnD games is the use of 20-sided dice (or d20 in dice notation) to determine the outcome of certain events^[1].

While there may be something mythical about one's fate being determined by Platonic solids^[2], the outcome of a dice roll follows discrete uniform distribution which has fairly large variance. I've seen a comment that compared DnD rules with other turn-based strategy games and complained that too much uncertainty makes it impossible to plan multiple steps ahead^[3]. The commenter promised to play the game only with mods.

Granted, uncertainly is part of the game (and part of life too), but how much uncertainty is appropriate? A single roll determining victory or demise may be thrilling for some but frustrating for others^[4]. Discrete uniform distribution is the maximum entropy distribution on N possible outcomes without other constraints, i.e. the most "uncertain". If a modder wants to reduce the uncertainty while keeping the dice mechanics, how may one implement it?

A simple way is to take the average of N independent rolls, which reduces the variance by a factor of 1/√N. For example, replacing 1d20 with 2d20/2. However, if we want the support (possible outcomes) to remain the same, we have to round the fractions to nearest integer(s). Note the possible plural, because .5 needs special treatment. If .5 are rounded in one direction^[5], the distribution will be skewed. The trick is to split the probability on .5 evenly to the integer below and above, keeping the symmetry, e.g.

P (2 d 20 / 2 = 1) = P (2 d 20 = 2) + P (2 d 20 = 3) / 2

P (2 d 20 / 2 = 2) = P (2 d 20 = 4) + P (2 d 20 = 3) / 2

1d20 has 5% probability for each outcome, with standard deviation 5.8; the distribution of rounded 2d20/2 is given below, with standard deviation 4.1 and 51% chance that the outcome falls in [8,13].

Outcome	Probability
1, 20	0.5%
2, 19	1.5%
3, 18	2.5%
4, 17	3.5%
5, 16	4.5%
6, 15	5.5%
7, 14	6.5%
8, 13	7.5%
9, 12	8.5%
10, 11	9.5%

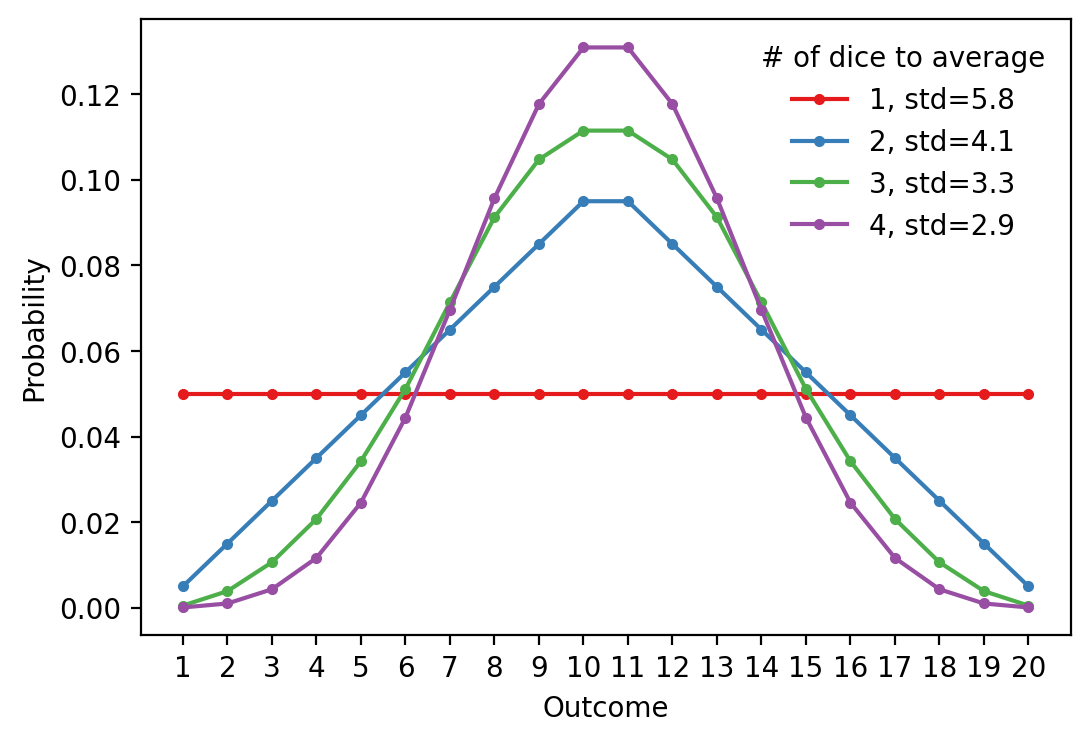
With 2 dice, the probability increases linearly towards the mean. With more dice, the distribution approaches normal distribution by central limit theorem. 2d20/2 seems to be easy enough to grasp and have sensible probabilities^[6]. The linearity should also be familiar to players that have seen 2-dice rolls.

The flat distribution does have one advantage though -- the cumulative distribution is linear. When 1d20 is rolled, its outcome is added to an "ability number". If the sum >= "difficulty number", the action succeeds. This means that every +1 in "ability number" results in +5% success chance. With 2 or more dice, this relation is no longer linear. The increase in "ability number" has greatest effect when success chance is around 50%. This is the case in Disco Elysium, where skill checks are performed with 2d6. (Remember those drugs?)

In any case, the commenter was not alone in disliking uncertainty. Einstein once said "I, at any rate, am convinced that He does not throw dice". Whether or not uncertainty is a fundamental feature of reality, it is definitely a useful model of world. One has to live with it and deal with it.

"Or maybe it's the entire world that's cursed? It's such a precarious place. Nothing ever works out the way you wanted."
"That's why people like role-playing games. You can be whoever you want to be. You can try again. Still, there's something inherently violent even about dice rolls."
"It's like every time you cast a die, something disappears. Some alternative ending, or an entirely different world..."
-- Novelty Dicemaker, Disco Elysium

Wish you a sweet roll.

In DnD 5e, d20 is used in 3 cases: (1) ability check, whether a character succeeds in a certain task; (2) attack roll, whether a weapon attack hits the target; (3) saving throw, whether a character avoids harmful effects. (Why do they have to use three different nouns for similar actions?) In addition, weapon damage is determined by damage roll using different kinds of dice depending on the weapon type. See here for a video introduction. ↩︎
In geometry, a Platonic solid is a convex, regular polyhedron in three-dimensional Euclidean space. Being a regular polyhedron means that the faces are congruent regular polygons, and the same number of faces meet at each vertex. (Wiki) There are only 5 such polyhedra: tetrahedron (d4), cube (d6), octahedron (d8), dodecahedron (d12), icosahedron (d20). d10 does not have these two properties. ↩︎
I can't find the exact review again due to a deluge of new reviews and lack of search feature on Steam. ↩︎
Or thrilling when the outcome is in their favor and frustrating when not. Also, failure often means reload, which rather defies the purpose. ↩︎
I only learned recently that in Python .5 is rounded to the nearest even number to avoid accumulation of rounding error, e.g. round(0.5) is 0, round(1.5) is 2. But this doesn't help in our case. ↩︎
One may even interpolate between 1dX and 2dX/2 distributions. I propose the name "house distribution" due to its shape, with parameters "base height" and "roof height" (min and max probabilities). ↩︎